Linear Search Methods are a integral part of numerical optimisation, which is a set of algorithms to solve mathematics programming problems. Importantly, numerical optimisation are solved in two key methods;

• Linear search strategy
• Trust region

This blog post will focus on the linear search strategy for optimisation techniques. This blog post requires a basic understanding on optimisation - objective functions, variables and constrained, so lets get into it.

What is line search and trust region, how do they differ?

Our main goal with optimsiation is to find a global minimimum points which in real life minimum point which reduced the time, cost etc. Now given we can algebraically find this optimal solution through other optimisation techniques. Let’s see an example,

Now, if we were to use algebratic methods using First order sufficient condition we find the unconstrained stationary point by $\triangledown f(\mathbf{x}) = \mathbf{0}$. But,

So the only way to finding a $ x $ algebratically is through guessing possible $ x $ values, even though the solution exists,

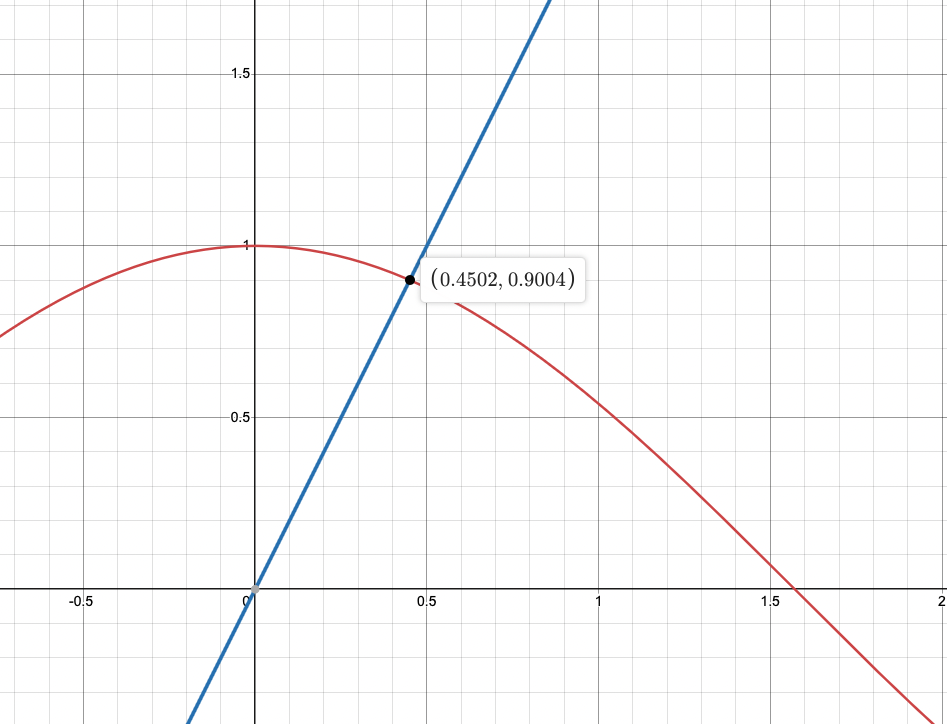
So this is where numerical optimsiation comes in. In essense rather then using algebraic methods to solve the optimisation problem we now is iterative process through a starting point $ x^{(0)} $ and then generatign a sequecnes of sets $ x^{(k)} $ which termiantes when a global minimum is reached, $ x^* $. Finding a new iteration step $ x^{(k)} $ is through finding where the rule of function value decreases known as decent methods,

We denote $ s^{(k)} $ as a search direction, which is is just given a point, $ x^{(k)} $ in which direction we move in? so intutively with no restricstion $ s^{(k)} $ can be in all directions from at point $ x^{(k)} $. Now, since restricitions imposed on $ x^{(k)} $ is the decent method how do apply this?

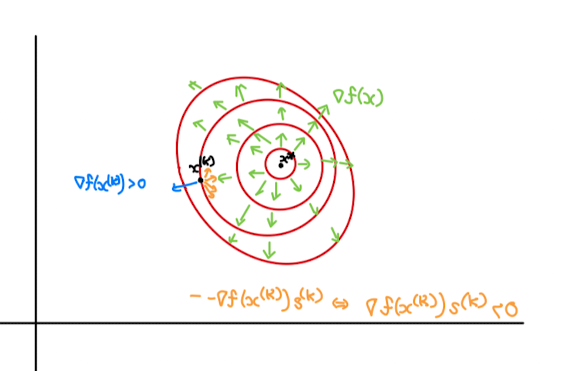
Definition : At a point $ x^{(k)} $ , a direction $ s^{(k)} $ is a descent direction if

Why?

Now $\triangledown f(x) $ points in direction of , so by taking $ - \triangledown f(x) $ we point any $ x $ to direction of steepest descent. So, $ \triangledown f(x^{(k)})^T s^{k} < 0 $.

So, since we know that $ s_{(k)} $ can be in any direction then to restirict we want all search direction which ensures we are in descent getting closer to minimiser ,

Intitively, we want to next iteration to be $ x^{(k + 1)} $ to be as a know in ferences to out previous iteration, $ x^{(k)} $, and $ s^{(k)} $, but since our search direction is also a vector direction we we dont impose a ‘length’ the search direction can be then we can overeach out minimiser $ x^* $

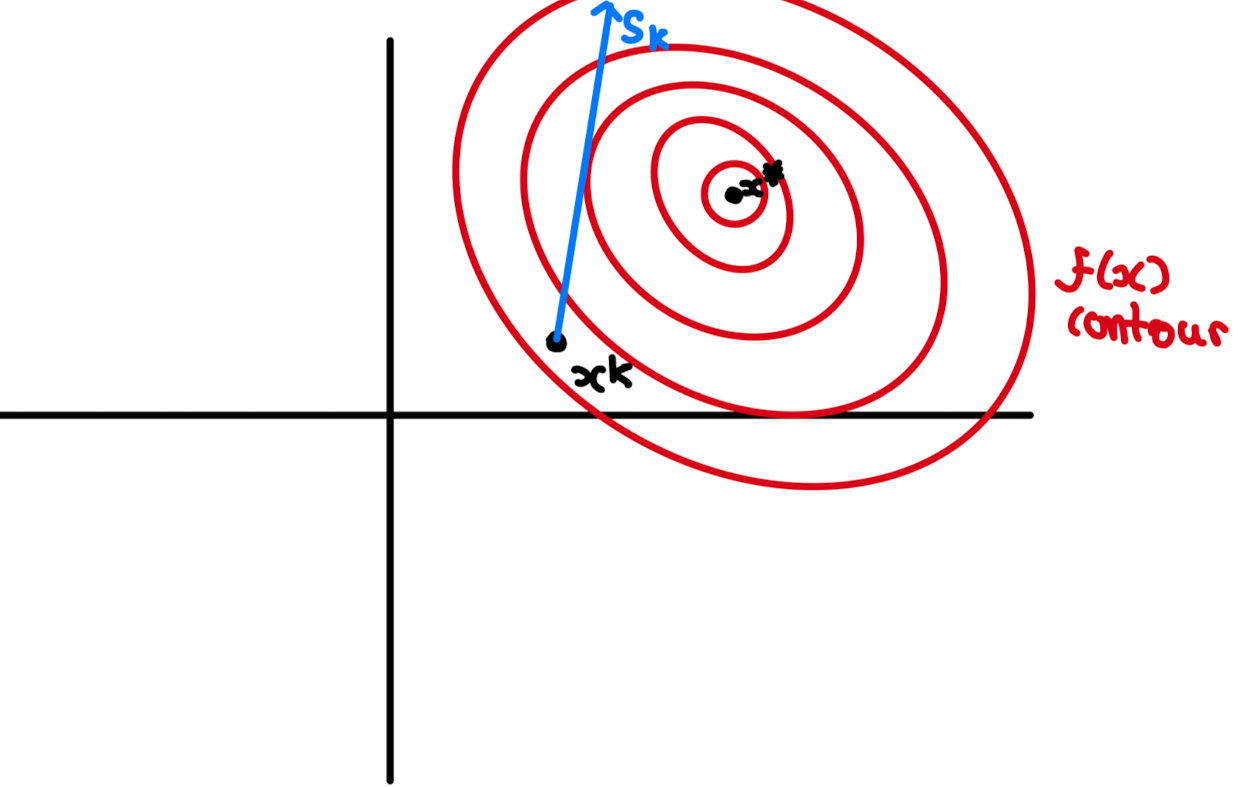
So we impose a step length $ \alpha_{k} $, in most algorithms, we will chose a step-size and after eahc iterations we optimise the step-size inrdoer to find the optimal ‘jump’ we want to impose.

Therfore by definition $ s^{(k)}$ is in decent direction of $ x^{(k)} $, if $ f(x^{(k)} + \alpha s^{(k)}) < f(x^{(k)})$ where we define $ x^{(k + 1)} = x^{(k)} + \alpha s^{(k)} $. Our goals is to prove that this is try using our definition of decent direction.

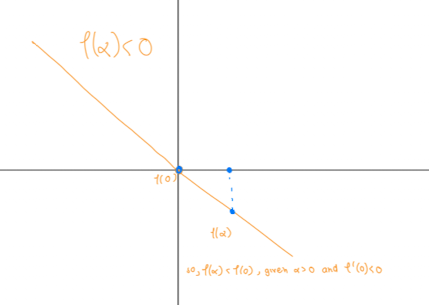
Let $ l(\alpha) = f(x^{(k)} + \alpha s^{(k)}) $ then $ \frac{d}{dx}(l(\alpha)) = \frac{d}{dx}f(x^{(k)} + \alpha s^{(k)}) $ when $ x^{(k)} = 0$ then, intuitively, if we can show that $ l’(\alpha) < 0 \Rightarrow l(\alpha) < l(0) \Rightarrow f(x^{(k)} + \alpha s^{(k)}) < f(x^{(k)}) $. Visually, in $\mathbb{R}^2$ for this to hold true then ,

So, since $ x^{(k)} \in \mathbb{R}^n $ we have to use the chain rule to find $ \frac{d}{dx}f(x^{(k)} + \alpha s^{(k)}) $. Let $x_{i}(\alpha) = x_{i}^{(k)} + \alpha s_{n}^{(k)}$ for all $ i \in \mathbb{Z^+} $ and for a fixed $ x^{(k)}, s^{(k)} $ we have,

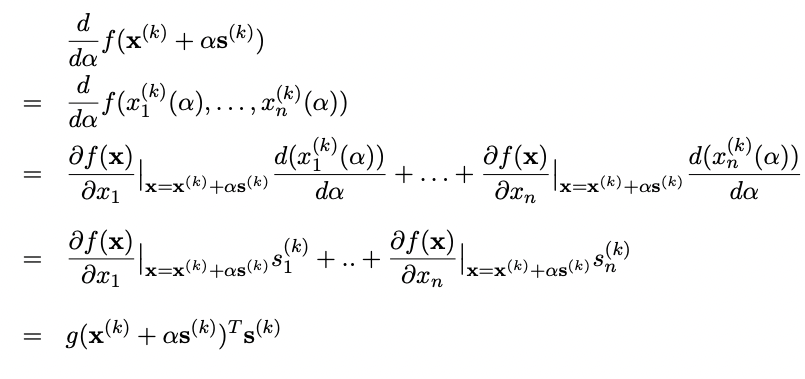
Then applying $ \alpha = 0 \Rightarrow l’(0) = f(x^{(k)})^Ts^{(k)} $. Now given $ s^{(k)} $ is in decent direction then $ l’(0) = f(x^{(k)})^Ts^{(k)} < 0 $ so hence, $ f(x^{(k)} + \alpha s^{(k)}) < f(x^{(k)}) $

How do we ensure that we pick a point $ x^{(k+1)} $ such that $ f(x^{(k)} + \alpha s^{(k)}) $ is closest to $ x^* $?

Finally, the process is known line search strategy which by definition is

Importantly, this is known as exact line search since, finds the optimal step size that minimizes the objective function along the search direction. But there exsit different types of line search including Backtracking Line Search, Golden Section Search, interpolation-Based Line Search. All these line search play around with step size, $ \alpha $ to find the most optimal method to minimer objective function.