Understanding the Roles/Links between Samples, Inference and Learning Models

I’v alway been confused of the role of statistical inference, sampling and learning models and how they all connect together. Although, I know statistical inference, it was unfortunately taught in a black box, so i always felt little incomplete when i begin learning Machine learning and modern statistical inference. How do these two connect? Well hopefully i can bridge this gap!

Sampling? Who are you

When learning about phenomenon’s we want to study we ask everyone in the best method would be to ask population right, so the population;

• Set of all elements from who the sample will be drawn Unfortunately, this is not always possible because of financial resource issues. But in some cases it is done, when? Umm election? Everyone in the population has to vote on who there president is, but the question to ask is how does this news corporations show polls of potential presidential ranking before the election is finished? Well they take the proportion of the population a.k.a sample and hope this sample is a reflection of the whole population!

What are different ways these news corporation could sample?

Generally when taking sample there are two main issues; (1) Sample Bias - based on the individuals in our sample we can bias a certain outcome which can include selection bias, response bias, nonresponsive bias (2) Chance error - random samples can vary from what is expected in any direction

General steps would be creating a sample is;

1. Identify our population

2.Create a sampling frame

a subset of population of potential people who can be in our sample

3.Chose a sampling scheme

note sampling method quality is more important then sampling size a few sampling methods includes;

• Convenience sample: is whoever is available we take them as our sample, but this has high bias
• Deterministic Sampling: When we specifically choose from our sampling frame, no chance
• probability/random sample : Given a sampling frame we give ‘chance’ of anyone being selected in our sample, thus there is a randomness about this. Through the use of probability we can know measure errors and thus we have reduced bias by not sampling non-randomly. The most common random sampling methods are
  • Systematic sample : randomly align all potential individuals in a line, then random choose from the start of sequences and then evenly choose between each individual to create the sample
  • uniform random sample with replacement : uniformly at random with replacement, but the problem is some people may be picked more then once!
  • simple random sample : sample drawn uniformly at random without replacement.
  • stratified random sample : where random sampling are performed on specific group, which each group is combined into a sample , thus stop the unbalanced class!

Given we have our sample how does new corporation make predictions about population

A ‘statistic’ , a number calculated from the sample and a ‘parameter’, a number associated with the population, now a statistic can be calculated from our sample can be used as an estimate of our ‘parameter’ which we cant feasible measure . Think Sample Mean vs Population Mean, \(\overline{X_n}\) and \(\mu\). Here Sample Mean is our statistic which estimates the population mean.

Now defining statistical inference; is using our ‘random sample’ we make conclusion about the population, i.e our we hope our sample mean is close to the population mean which we don’t know. How can we check our sample statistic/estimator is close to our population paramter?

1. Variance: How does my statistic changes with each sample: \(Var(\theta) = \mathbb{E}((\hat{\theta} - \theta)^2)\)
2. Bias : Did we get the right answer to our parameter? \(Bias(\hat{\theta})= \mathbb{E}(\hat{\theta} - \theta)\)
3. Risk/MSE = Variance + Bias^2 : How close is our parameter ? \(MSE(\hat{\theta}) = \mathbb{E}(\hat{\theta} - \theta)^2\)

So for our new coporation they will want to find the sample mean for votes for say trump.

Learning Models

Now, when building models we have either two goals, (1) Prediction of unseen data, regression or classification (2) Inference: draw conclusions about the underlying relationships between features and response, so training is the process of fitting a model while inference is making the prediction

Now lets take an example, suppose we have a simple linear regression, our population parameter is which we want to find but we don’t know,

\[\begin{align*} y = \beta_0 + \beta_1 x_0 \end{align*}\]

Now using our random sample we get our estimated parameters,

\[\begin{align*} y &= b_0 + b_1 x_0 \Longleftrightarrow \\ y &= 9.3 + 4.3 x_0 \end{align*}\]

Okay so our estimated statistic/estimator \(b_1 = 4.3\) so then can we conclude that our parameter is \(\beta_1 = 4.3\) ? Is this right? No! Well not right now we only considered 1 random sample, we could have totally got it wrong, since we hadn’t compared it to any other samples!

So to find the true parameter \(\beta_1\) we make conclusion from the distribution/probability of statistic \(b_1\) from all possible random samples! And then we use hypothesis testing check check if potentially is \(\beta_1 = 4.3\).

How can we do this hypothesis testing?

Outlined in “Computation Age of Statistical Inference” by Bradley Efron and Trevor Hastie, we can check our estimator from classifical statistical inference methods like Taylor-series approximations, plug-in principle to modern methods including bootstrapping, Jackknife resampling.

Let’s take Jackknife resampling. \

This is a resampling method invented by Quenouille in 1949 for the sole purpose of reducing bias of estimators! In this method since it is always difficult to resample from the population, so jackknife resampling takes N-subsample, in each subsample 1 individual taken out each time so the subsample size is always N - 1, since we have N individuals in our original sample, thus the every individual in the original sample is taken out atleast once. Then we do our simple linear regression again and get our \(b_1\) statistic, a estimate of our parameter \(\beta_1\), we then taken the mean of all \(b_1\) from each sample

\[\begin{align*} \overline{b_1} = \frac{1}{n - 1} \sum_{i = 1}^n b_{1,i} \end{align*}\]

Therefore, we know from our subsample some \(b_1\) will over shoot our original parameter and some subsample \(b_1\) will undershoot, but we hope on average \(\overline{b_1} = \beta_1\) .

Since, we have a range of \(b_1\) values we can create a empirical probability density distribution graph and then find 95% confidence interval \(b_1\) So our hypothesis is \(\begin{align*} H_0 &: b_1 = 4.3 \\ H_a &: b_1 \neq 4.3 \end{align*}\)

So we conduct jackknife sampling to find the jackknife empirical distribution of statistic \(b_1\);

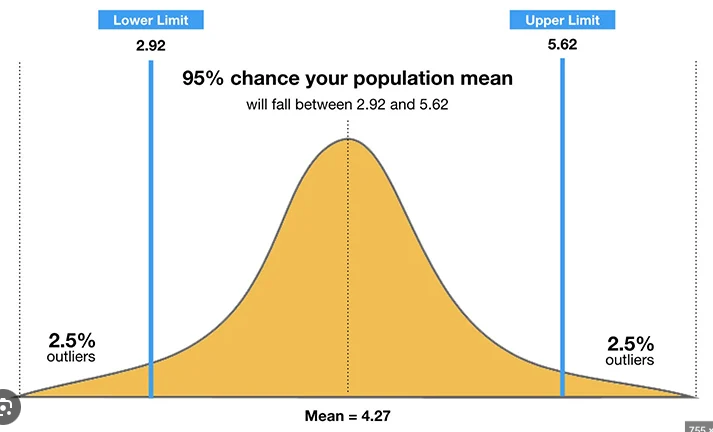
Clearly,

\[CI(b_0) = [2.92, 5.62] = [2.5\%, 97.5\%]\]

so we don’t have enough evidence to reject our null hypothesis. Thus our regression model is valid

\[\begin{align*} y &= 9.3 + 4.3 x_0 \end{align*}\]

Note : if our model doesn’t hold say, the relationship between y and x is not linear then the inference also doesn’t hold!

So now we have a learning model which holds true and thus we can predict future values of \(y\) using \(x_0\)

Conclusion

Now both you and me both understand the relationship between sampling, inference and learning models!